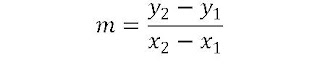NOTA: En esta ocasión será necesario que LAS DOS TAREAS sean entregadas en PDF, porque el tiempo de revisión disponible para mí será muy corto, y ahorraré mucho tiempo al corregir documentos PDF. Si aun no sabes cómo hacerlo, al final de la entrada tienes varias recomendaciones para crear un documento PDF. La presentación del documento en PDF se incluye en la rúbrica de evaluación.
Espacio virtual destinado al refuerzo de los conocimientos de matemáticas de los estudiantes del Colegio Kalil Gibrán.
jueves, 4 de junio de 2020
FACTORIZACIÓN
Etiquetas:
Agrupación de términos,
Factor común,
Factores,
Factorización,
Gibrán,
Kalil,
Matemáticas
Ubicación:
El Tigre 6050, Anzoátegui, Venezuela
martes, 19 de mayo de 2020
ANÁLISIS COMBINATORIO
Bienvenidos, esta entrada está dedicada a un análisis matemático que será de utilidad ante situaciones de la vida diaria,en los estudios universitarios y en el entorno profesional.
En esta ocasión, la la entrada ha incorporado algunas estrategias nuevas, por lo que se pide al lector que revise todo lo escrito hasta el final de la publicación. Se han implementado mejoras y a los representantes se les ha dejado una nota especial al final de la entrada.
PRESENTACIÓN DEL TEMA
Ante de desarrollar el tema, respondamos algunas interrogantes interesantes...
¿Qué es el análisis combinatorio o la combinatoria?
La combinatoria es una rama de las matemáticas cuyo objeto es estudiar las posibles agrupaciones de objetos que podemos llevar a cabo de un modo rápido teniendo en cuenta las relaciones que deben existir entre ellas.
¿Par qué sirve la combinatoria?
La teoría del análisis combinatorio nos puede ayudar a resolver diversos "problemas de conteo", tanto en la vida diaria como en el entorno profesional.
Se aplica en aquellas situaciones donde distintas maneras de agrupar un número determinado de elementos tenga importancia.
¿Cuáles son las aplicaciones de la combinatoria?
Por nombrar algunos ejemplos, les cito los siguientes:
- La manera en que podríamos ordenar a un grupo de personas para desarrollar una actividad específica.
- Las diferentes formas en que podría quedar estructurada una junta directiva en una organización o empresa de varias personas, asignando los cargos.
- Maneras diferentes de arreglar un conjunto de adornos en una mesa.
- Cantidad de números de teléfonos para una comunidad, a partir de x cantidad de dígitos dados, etc.
domingo, 19 de abril de 2020
Análisis de Funciones
En esta entrada nos dedicaremos a revisar los pasos que se realizan para representar correctamente una gráfica, tomando como punto de partida la función más sencilla de graficar, la "función afín".
PRESENTACIÓN DEL TEMA
En las matemáticas, una de las actividades que se presentan con cierta frecuencia es la de la representación gráfica de funciones, que a su vez provienen del resultado de analizar el comportamiento de algún fenómeno o proceso físico o social...
Entonces, es preciso tener los conocimientos que nos permitan llevar a la representación visual este comportamiento para ampliar las posibilidades de análisis.
Etiquetas:
afín,
concavidad,
coordenadas,
creciente,
decreciente,
funciones,
gráfica,
pendiente,
plano cartesiano,
recta
Ubicación:
El Tigre 6050, Anzoátegui, Venezuela
lunes, 6 de abril de 2020
PLAN DE EVALUACIÓN DE 3ER LAPSO
Buenas tardes apreciados estudiantes.
En cumplimiento de los lineamientos de organización, planificación y evaluación necesario para la educación en el Tercer Año de Bachillerato, en esta publicación coloco el correspondiente Plan de Evaluación.
Esta imagen se puede descargar en el siguiente enlace:
En él se establecen los lapsos de entrega para cada una de las 4 asignaciones, y las fechas de entrega de las clases transcritas en los cuadernos de matemáticas.
Para cada tema, en la semana de recepción primero se recibirán las asignaciones (en lunes y martes) y luego se recibirá la transcripción de la clase en el cuaderno de matemáticas (el día viernes).
Las consultas iniciales siguen como se planteó desde un principio, vía email y whatsapp, en el horario pautado.
Ahora, como mecanismo extra de apoyo, el docente podría ofrecer una clase para las consultas sobre el tema de la asignación. Se trata de una Clase - Chat por Whatsapp en la que durante un tiempo máximo de 2 horas, se atenderán las consultas de los estudiantes que estén en el grupo organizado (cada sección por separado).
Se plantea esta clase como una alternativa y no como una obligación de los estudiantes, y su realización se limita a una sola vez por asignación, con la condición previa de que los estudiantes ya hayan revisado y transcrito la clase publicada en el blog, de manera que se puedan generar dudas que consultar en la clase chat. Debido a esto, la clase podrá pautarse a partir de la semana siguiente a la publicación de la clase/asignación, dando tiempo de la preparación de los estudiantes.
Para fijar el día y la hora de la sesión de consulta, en docente y los representantes de cada sección se pondrán de acuerdo, con anticipación.
Sin más que agregar, me despido.
¡Si todos colaboramos, la tempestad pasará en menos tiempo, y volveremos a la normalidad. Mantengámonos unidos!
M.Sc. Ernesto Vaquero
Matemáticas UEP Kalil Gibrán
miércoles, 1 de abril de 2020
ANÁLISIS EN EL PLANO
Bienvenidos nuevamente a este espacio.
En esta ocasión abordaremos un tema sencillo que involucra los conocimientos fundamentales del plano cartesiano.
PRESENTACIÓN DEL TEMA
El el sistemas de coordenadas cartesianas en dos dimensiones (plano cartesiano), es posible representar diversas formas, funciones o simplemente coordenadas de puntos en particular. En esta oportunidad vamos a iniciar el estudio de un segmento, lo graficaremos, le encontraremos el punto medio y también su longitud, entre otras cosas... Todo a partir de unas sencillas fórmulas que se podrán aprender con la práctica. Entremos en materia.
TEORÍA + EJERCICIOS
En geometría, el segmento es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales.
REPRESENTACIÓN DE UN SEGMENTO
En nuestro estudio, como datos, se conocen inicialmente las coordenadas de estos extremos, y con ellos se facilita la representación del segmento en el plano.
Veamos un ejemplo:
Dados los puntos A(1,2) y B(6,4) trazar el segmento AB.
Al llevar los puntos A y B al plano cartesiano se vería de la siguiente manera:
Para representar el segmento AB simplemente se deben unir los puntos A y B con una regla y listo. Se debe ver de la siguiente manera:
Es un proceso simple, que se puede realizar tomando cualquier par de puntos ubicados en cualquiera de los cuadrantes, veamos un ejemplo más.
Representar el segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4)
Vamos directamente a representar los dos puntos y a trazar el segmento, para obtener el siguiente resultado:
Ahora que tenemos claro cómo llevar al plano un segmento, tenemos que aprender a determinar algunas caraterísticas del mismo. A continuación analizaremos 3 características muy importantes que se derivan del análisis de un segmento cualquiera:
- Longitud de un segmento
- Punto medio de un segmento
- Pendiente asociada a un segmento (Pendiente de la recta que lo contiene)
Veamos el primero...
LONGITUD DE UN SEGMENTO
A todos los segmentos se le puede calcular su longitud, y esto se logra mediante una operación matemática que no necesita usar el plano, sino una pequeña fórmula, derivada del conocido Teorema de Pitágoras.
La fórmula en cuestión es la siguiente:
LS: Longitud del Segmento
X1 y Y1 corresponden a los valores del primer extremo del segmento.
X2 y Y2 corresponden a los valores del segundo extremo del segmento.
Obsérvese que dentro de la raíz, las restas que se realizan ocurren sólo entre elementos de la misma naturaleza (las "X" con las "X" y las "Y" con las "Y").
Otra manera de denominar este concepto es llamarlo "distancia entre dos puntos", que en nuestro caso serían los puntos A y B.
La Expresión tendría un pequeño cambio:
(es en el fondo la misma fórmula)
Veamos un ejemplo retomando el caso del principio:
Dados los puntos A(1,2) y B(6,4) hallar la longitud del segmento AB.
Para esto, debemos identificar las coordenadas X y Y de cada punto.
Del punto A tenemos:
X1: 1
Y1: 2
Del punto B tenemos:
X2: 6
Y2: 4
Entonces ahora es momento de usar la fórmula anterior, sustituyendo los datos anteriores...
Al resultar una raíz inexacta, la podemos dejar expresada tal como está.
Veamos un segundo ejemplo, tomando el segundo caso del principio.
Del segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4), hallar la longitud.
Nuevamente debemos identificar los valores de X y Y para cada unos de los puntos A y B, para luego meterlos en la fórmula de la longitud del segmento.
Del punto A tenemos:
X1: -5
Y1: 1
Del punto B tenemos:
X2: 3
Y2: -4
Usando la fórmula, los pasos serían los siguientes:
Nuevamente se deja así la raíz.
Ahora vamos a conocer la manera descubrir cuál es exactamente el "punto medio" de un segmento...
PUNTO MEDIO DE UN SEGMENTO
Esta parte del estudio, lleva representación gráfica. Sin embargo, requiere de un trabajo previo con unos sencillos cálculos que nos permitirán conocer "cuál" es la ubicación del punto medio de un segmento, es decir, sus "coordenadas" X y Y.
Para esto utilizaremos las siguientes fórmulas:
donde
y
Los valores XM y YM representan las coordenadas del punto medio del intervalo.
Veamos un ejemplo:
(nuevamente retomemos el primer ejemplo)
Dados los puntos A(1,2) y B(6,4) calcular y representar el Punto Medio del Segmento AB.
Vayamos directamente al cálculo, de las tres fórmulas mostradas recientemente, usaremos la segunda y la tercera:
Del punto A tenemos:
X1: 1
Y1: 2
Del punto B tenemos:
X2: 6
Y2: 4
y calculamos,
así,
XM: 3,5
YM: 3
Estas coordenadas se usan en la primera de las tres fórmulas, para expresar el Punto Medio:
Ahora, si tomamos ese punto y lo llevamos a la gráfica donde ya estaba trazado el segmento AB, el resultado se vería de la siguiente manera:
Veamos el segundo ejemplo
Del segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4), calcular y representar el Punto Medio.
De nuevo vamos a emplear las fórmulas anteriores, en el mismo orden, y antes vamos a identificar las coordenadas de A y B para poder meterlas en las fórmulas.
Del punto A tenemos:
X1: -5
Y1: 1
Del punto B tenemos:
X2: 3
Y2: -4
y calculamos,
así,
XM: -1
YM: -1,5
Estas coordenadas se usan en la correspondiente fórmula para expresar el Punto Medio:
Ahora, si tomamos ese punto y lo llevamos a la gráfica donde ya estaba trazado el segmento AB, el resultado se vería de la siguiente manera:
Finalmente, para cerrar la teoría, vamos a estudiar la pendiente asociada a un segmento.
PENDIENTE ASOCIADA A UN SEGMENTO
Toda línea recta tiene por definición una "pendiente", es decir, un grado de inclinación que la carateriza.
Recordemos que la pendiente de una recta se representa con la letra "m"
Según WIKIPEDIA, En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento lineal, natural o constructivo respecto de la horizontal.
Recordando que en este tema estamos asumiendo que los puntos A y B se están suminstrando de antemano, por lo que la forma más pertinente de obtener la pendiente es la siguiente:
Al observar la fórmula, se sabe que con sólo saber las coordenadas de los extremos de cualquier segmento, será posible determinar su pendiente.
El cálculo de la pendiente, es un procedimiento analítico y se apoya un poco en la parte gráfica, pero no lleva mayor peso en la representación.
Veamos el primer ejemplo:
Continuando el primer ejemplo del principio,
Dados los puntos A(1,2) y B(6,4) determinar la pendiente del Segmento AB.
En este caso, como sbemos
Del punto A tenemos:
X1: 1
Y1: 2
Del punto B tenemos:
X2: 6
Y2: 4
sustituimos en la fórmula de la pendiente,
m = 0,4 o simplemente 2/5
De los conocimientos anteriores es muy importante recordar lo siguiente:
1.- Cuando la pendiente es positiva, la línea tiene un trazo "creciente" (Se puede intrepretar que el segmento o recta va "subiendo" con el aumento de x)
2.- Cuando la pendiente es negativa, la límea tiene un trazo "decreciente" (Se puede intrepretar que el segmento o recta va "bajando "con el aumento de x)
Del resultado anterior, m = 2/5, se desprende que la pendiente es positiva, y coincide perfectamente con la dirección del segmento trazado originalmente.
Veamos el último ejemplo:
Del segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4), determinar la pendiente.
Nuevamente emplearemos la fórmula de la pendiente.
Del punto A tenemos:
X1: -5
Y1: 1
Del punto B tenemos:
X2: 3
Y2: -4
y calculamos,
m = -0,625 o simplemente -5/8
Del resultado anterior, m = -5/8, se desprende que la pendiente es negativa, y coincide perfectamente con la dirección del segmento trazado originalmente.
EJERCICIOS DE PRÁCTICA
Con la intención de fortalecer sus habilidades sobre este tema, y prepararlos para una exitosa elaboración de la asignación, es preciso que desarrollen los siguientes ejercicios completos en casa, los cuales deben ser copiados en el cuaderno junto a toda la teoría y los ejemplos.
Ejercicios de práctica:
- Dados los puntos A(0,7) y B(6,-2), represente el segmento AB en el plano, determine su longitud, calcule y represente su Punto Medio y determine la pendiente asociada al segmento.
- Dados los puntos A(-5,-3) y B(2,4), represente el segmento AB en el plano, determine su longitud, calcule y represente su Punto Medio y determine la pendiente asociada al segmento.
Como nota importante deben saber que:
COPIAR TODA LA TEORÍA Y EJEMPLOS MÁS LOS EJERCICIOS PROPUESTOS EN EL CUADERNO TIENEN UN VALOR DE 5%
(Estos serán posteriormente revisados para su evaluación)
A continuación se presenta una selección de ejercicios que deben ser resueltos en hojas blancas, y luego remitidos al docente en la fecha establecida para su posterior evaluación.
Lo primero es colocar una portada básica que lleve todos los datos de la asignación:
- Año académico
- Sección
- Nombre y Apellido del estudiante
- Número de la asignación (#1)
- Fecha de entrega
Ejercicios:
Para cada uno de los siguientes planteamientos, debe representar el segmento AB en el plano, determinar su longitud, calcular y representar su Punto Medio y finalmente determinar la pendiente asociada al segmento.
- A(-7,-4) y B(6,5)
- A(-4,8) y B(5,-2)
- A(-5,3) y B(4,-3)
- A(-6,2) y B(7,6)
- A(-4,4) y B(7,7)
Condiciones de elaboración y entrega de la asignación:
- Debe ser realizada a mano.
- Debe llevar los datos solicitados en la portada
- El plazo máximo de entrega es hasta el 13-14 de abril. (Todo el día).
- Las consultas finalizan el viernes de la semana previa a la entrega de la asignación.
- La asignación debe ser fotografiada y enviada al docente únicamente al correo electrónico.
- Pueden enviar el trabajo como un documento Word o PDF con la portada solicitada y las imágenes adentro.
Enviar al correo electrónico:
ernestovaquero@gmail.com
Dentro de las fuentes de información que hay en Internet, he traído algunas paora que sirvan de apoyo a la lectura de esta publicación.
- Distancia entre dos puntos (longitud del Segmento): Video distancia entre dos puntos
- Punto medio de un segmento: Video Punto Medio
- Pendiente a partir de dos puntos: Video pendiente de un segmento
Esto es todo por el tema de análisis en el plano.
Hasta la próxima entrada, y espero sus consultas.
¡Si todos colaboramos, la tempestad pasará en menos tiempo, y volveremos a la normalidad. Mantengámonos unidos!
M.Sc. Ernesto Vaquero
Matemáticas UEP Kalil Gibrán
Etiquetas:
cartesiano,
Gibrán,
Kalil,
Matemáticas,
medio,
pendiente,
Plano,
punto,
segmento
Ubicación:
El Tigre 6050, Anzoátegui, Venezuela
miércoles, 25 de marzo de 2020
FORMA DE TRABAJO EN 3ER LAPSO
Esta publicación está completamente dedicada a establecer las instrucciones de trabajo y las condiciones bajo las cuales se desarrollarán las actividades académicas a lo largo de este tercer lapso.
Se seleccionarán estrategias específicas, medios de difusión, formas de trabajo, mecanismos de consulta, y formas de recepción de las tareas asignadas de modo que tanto la instrucción como la evaluación llegue a todos los hogares con la mayor facilidad posible.
Próximamente estaré colocando una asignación referente al primer tema de trabajo de este lapso, especificando todas las condiciones en esa publicación, la cual será informada esta misma semana. Posteriormente se publicará todo el plan de evaluación para que se puedan planificar en función de cada uno de los temas contenidos en el período, las actividades asociadas y los lapsos de entrega de las asignaciones.
CONDICIONES GENERALES DE TRABAJO DE LAS ASIGNACIONES DE MATEMÁTICAS
- Las nuevas asignaciones se publicarán con regularidad cada tres jueves.
- Cada asignación tendrá un tiempo de 3 semanas para su elaboración y entrega.
- En el intermedio, los estudiantes/representantes contarán con un espacio para las interacción con el docente, en el cual se tratarán las inquietudes, dudas o consultas que se refieran al desarrollo de la asignación u otro detalle asociado a la elaboración o entrega misma.
- La recepción de las asignaciones o tareas será siempre en un lapso de 2 días para facilitar su entrega (lunes y martes), los cuales serán señalados al momento de colocación de cada asignación.
- El(los) mecanismo(s) de recepción será(n) indicado(s) en cada asignación,para que cada quién utilice el que se le haga más fácil.
- Correo electrónico.
- Whatsapp.
- Otros.
- Sólo se debe emplear uno de los mecanismos de entrega de la tarea, para evitar duplicar envíos de tareas.
- En cada tarea estará señalada la modalidad de trabajo:
- Elaboración a mano (en el cuaderno)
- Elaboración a mano (en hojas blancas)
- Elaboración a computadora, con el formato señalado (Word, powerpoint, imagen, entre otros)
- Otra
- Cuando presentar la actividad para su entrega requiera tomar fotografías, es necesario que las imágenes sean tomadas con nitidez.
- Al entregar una tarea es necesario que esta contenga toda la identificación del estudiante dentro de su propia elaboración (sea una fotografía o un trabajo digital), para que la misma sea independiente del medio de envío, y sea fácil de organizar para su evaluación.
- Los datos necesarios en la entrega de cada asignación son:
- Año académico,
- Sección,
- Nombre y apellido,
- # de la asignación,
- Fecha de entrega.
- La calificación de las asignaciones será informada oportunamente, en un período posterior de una semana después del lapso de entregas.
- En el caso de que algún estudiante presente alguna condición especial de trabajo que dificulte la realización de las actividades de evaluación, deberá comunicarse directamente conmigo, a través del correo electrónico o por teléfono para luego plantear su situación ante la coordinación de evaluación y canalizar la alternativa correspondiente.
HORARIO Y MECANISMOS DE CONSULTA
Con el propósito de establecer un canal sólido para la interacción entre estudiantes y docente, se establecerá un horario de consulta en el cual podrán ponerse en contacto conmigo y señalar todas las inquietudes que tengan. Por esa vía recibirán las correspondientes orientaciones para asegurar que tengan claras todas las indicaciones para el desarrollo de sus actividades.
Horario de consulta:
En la imagen se muestra el horario en el cual los estudiantes y representantes podrán comunicarse con el docente para cualquier tema en relación con las instrucciones, asignaciones, entrega y evaluación, entre otras cosas.
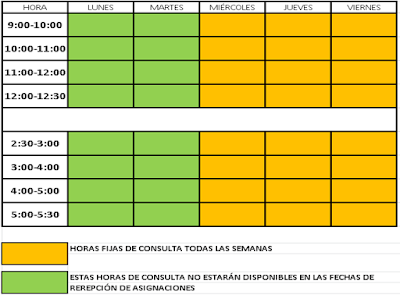
Los medios de consulta disponibles inicialmente serán el correo electrónico y el chat de whatsapp.
Se está evaluando la posibilidad de establecer un foro de discusión web por año para las consultas, en el cual se puedan discutir temas específicos para aclarar dudas, la preparación de esto puede tomar algo de tiempo.
Mi correo electrónico es:
ernestovaquero@gmail.com
A partir de la próxima entrada se publican las asignaciones, hasta pronto.
¡Si todos colaboramos, la tempestad pasará en menos tiempo, y volveremos a la normalidad. Mantengámonos unidos!
M.Sc. Ernesto Vaquero
Matemáticas UEP Kalil Gibrán
Suscribirse a:
Comentarios (Atom)