Bienvenidos nuevamente a este espacio.
En esta ocasión abordaremos un tema sencillo que involucra los conocimientos fundamentales del plano cartesiano.
PRESENTACIÓN DEL TEMA
El el sistemas de coordenadas cartesianas en dos dimensiones (plano cartesiano), es posible representar diversas formas, funciones o simplemente coordenadas de puntos en particular. En esta oportunidad vamos a iniciar el estudio de un segmento, lo graficaremos, le encontraremos el punto medio y también su longitud, entre otras cosas... Todo a partir de unas sencillas fórmulas que se podrán aprender con la práctica. Entremos en materia.
TEORÍA + EJERCICIOS
En geometría, el segmento es un fragmento de recta que está comprendido entre dos puntos, llamados puntos extremos o finales.
REPRESENTACIÓN DE UN SEGMENTO
En nuestro estudio, como datos, se conocen inicialmente las coordenadas de estos extremos, y con ellos se facilita la representación del segmento en el plano.
Veamos un ejemplo:
Dados los puntos A(1,2) y B(6,4) trazar el segmento AB.
Al llevar los puntos A y B al plano cartesiano se vería de la siguiente manera:
Para representar el segmento AB simplemente se deben unir los puntos A y B con una regla y listo. Se debe ver de la siguiente manera:
Es un proceso simple, que se puede realizar tomando cualquier par de puntos ubicados en cualquiera de los cuadrantes, veamos un ejemplo más.
Representar el segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4)
Vamos directamente a representar los dos puntos y a trazar el segmento, para obtener el siguiente resultado:
Ahora que tenemos claro cómo llevar al plano un segmento, tenemos que aprender a determinar algunas caraterísticas del mismo. A continuación analizaremos 3 características muy importantes que se derivan del análisis de un segmento cualquiera:
- Longitud de un segmento
- Punto medio de un segmento
- Pendiente asociada a un segmento (Pendiente de la recta que lo contiene)
Veamos el primero...
LONGITUD DE UN SEGMENTO
A todos los segmentos se le puede calcular su longitud, y esto se logra mediante una operación matemática que no necesita usar el plano, sino una pequeña fórmula, derivada del conocido Teorema de Pitágoras.
La fórmula en cuestión es la siguiente:
LS: Longitud del Segmento
X1 y Y1 corresponden a los valores del primer extremo del segmento.
X2 y Y2 corresponden a los valores del segundo extremo del segmento.
Obsérvese que dentro de la raíz, las restas que se realizan ocurren sólo entre elementos de la misma naturaleza (las "X" con las "X" y las "Y" con las "Y").
Otra manera de denominar este concepto es llamarlo "distancia entre dos puntos", que en nuestro caso serían los puntos A y B.
La Expresión tendría un pequeño cambio:
(es en el fondo la misma fórmula)
Veamos un ejemplo retomando el caso del principio:
Dados los puntos A(1,2) y B(6,4) hallar la longitud del segmento AB.
Para esto, debemos identificar las coordenadas X y Y de cada punto.
Del punto A tenemos:
X1: 1
Y1: 2
Del punto B tenemos:
X2: 6
Y2: 4
Entonces ahora es momento de usar la fórmula anterior, sustituyendo los datos anteriores...
Al resultar una raíz inexacta, la podemos dejar expresada tal como está.
Veamos un segundo ejemplo, tomando el segundo caso del principio.
Del segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4), hallar la longitud.
Nuevamente debemos identificar los valores de X y Y para cada unos de los puntos A y B, para luego meterlos en la fórmula de la longitud del segmento.
Del punto A tenemos:
X1: -5
Y1: 1
Del punto B tenemos:
X2: 3
Y2: -4
Usando la fórmula, los pasos serían los siguientes:
Nuevamente se deja así la raíz.
Ahora vamos a conocer la manera descubrir cuál es exactamente el "punto medio" de un segmento...
PUNTO MEDIO DE UN SEGMENTO
Esta parte del estudio, lleva representación gráfica. Sin embargo, requiere de un trabajo previo con unos sencillos cálculos que nos permitirán conocer "cuál" es la ubicación del punto medio de un segmento, es decir, sus "coordenadas" X y Y.
Para esto utilizaremos las siguientes fórmulas:
donde
y
Los valores XM y YM representan las coordenadas del punto medio del intervalo.
Veamos un ejemplo:
(nuevamente retomemos el primer ejemplo)
Dados los puntos A(1,2) y B(6,4) calcular y representar el Punto Medio del Segmento AB.
Vayamos directamente al cálculo, de las tres fórmulas mostradas recientemente, usaremos la segunda y la tercera:
Del punto A tenemos:
X1: 1
Y1: 2
Del punto B tenemos:
X2: 6
Y2: 4
y calculamos,
así,
XM: 3,5
YM: 3
Estas coordenadas se usan en la primera de las tres fórmulas, para expresar el Punto Medio:
Ahora, si tomamos ese punto y lo llevamos a la gráfica donde ya estaba trazado el segmento AB, el resultado se vería de la siguiente manera:
Veamos el segundo ejemplo
Del segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4), calcular y representar el Punto Medio.
De nuevo vamos a emplear las fórmulas anteriores, en el mismo orden, y antes vamos a identificar las coordenadas de A y B para poder meterlas en las fórmulas.
Del punto A tenemos:
X1: -5
Y1: 1
Del punto B tenemos:
X2: 3
Y2: -4
y calculamos,
así,
XM: -1
YM: -1,5
Estas coordenadas se usan en la correspondiente fórmula para expresar el Punto Medio:
Ahora, si tomamos ese punto y lo llevamos a la gráfica donde ya estaba trazado el segmento AB, el resultado se vería de la siguiente manera:
Finalmente, para cerrar la teoría, vamos a estudiar la pendiente asociada a un segmento.
PENDIENTE ASOCIADA A UN SEGMENTO
Toda línea recta tiene por definición una "pendiente", es decir, un grado de inclinación que la carateriza.
Recordemos que la pendiente de una recta se representa con la letra "m"
Según WIKIPEDIA, En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento lineal, natural o constructivo respecto de la horizontal.
Recordando que en este tema estamos asumiendo que los puntos A y B se están suminstrando de antemano, por lo que la forma más pertinente de obtener la pendiente es la siguiente:
Al observar la fórmula, se sabe que con sólo saber las coordenadas de los extremos de cualquier segmento, será posible determinar su pendiente.
El cálculo de la pendiente, es un procedimiento analítico y se apoya un poco en la parte gráfica, pero no lleva mayor peso en la representación.
Veamos el primer ejemplo:
Continuando el primer ejemplo del principio,
Dados los puntos A(1,2) y B(6,4) determinar la pendiente del Segmento AB.
En este caso, como sbemos
Del punto A tenemos:
X1: 1
Y1: 2
Del punto B tenemos:
X2: 6
Y2: 4
sustituimos en la fórmula de la pendiente,
m = 0,4 o simplemente 2/5
De los conocimientos anteriores es muy importante recordar lo siguiente:
1.- Cuando la pendiente es positiva, la línea tiene un trazo "creciente" (Se puede intrepretar que el segmento o recta va "subiendo" con el aumento de x)
2.- Cuando la pendiente es negativa, la límea tiene un trazo "decreciente" (Se puede intrepretar que el segmento o recta va "bajando "con el aumento de x)
Del resultado anterior, m = 2/5, se desprende que la pendiente es positiva, y coincide perfectamente con la dirección del segmento trazado originalmente.
Veamos el último ejemplo:
Del segmento cuyos extremos corresponden a los puntos A(-5,1) y B(3,-4), determinar la pendiente.
Nuevamente emplearemos la fórmula de la pendiente.
Del punto A tenemos:
X1: -5
Y1: 1
Del punto B tenemos:
X2: 3
Y2: -4
y calculamos,
m = -0,625 o simplemente -5/8
Del resultado anterior, m = -5/8, se desprende que la pendiente es negativa, y coincide perfectamente con la dirección del segmento trazado originalmente.
EJERCICIOS DE PRÁCTICA
Con la intención de fortalecer sus habilidades sobre este tema, y prepararlos para una exitosa elaboración de la asignación, es preciso que desarrollen los siguientes ejercicios completos en casa, los cuales deben ser copiados en el cuaderno junto a toda la teoría y los ejemplos.
Ejercicios de práctica:
- Dados los puntos A(0,7) y B(6,-2), represente el segmento AB en el plano, determine su longitud, calcule y represente su Punto Medio y determine la pendiente asociada al segmento.
- Dados los puntos A(-5,-3) y B(2,4), represente el segmento AB en el plano, determine su longitud, calcule y represente su Punto Medio y determine la pendiente asociada al segmento.
Como nota importante deben saber que:
COPIAR TODA LA TEORÍA Y EJEMPLOS MÁS LOS EJERCICIOS PROPUESTOS EN EL CUADERNO TIENEN UN VALOR DE 5%
(Estos serán posteriormente revisados para su evaluación)
A continuación se presenta una selección de ejercicios que deben ser resueltos en hojas blancas, y luego remitidos al docente en la fecha establecida para su posterior evaluación.
Lo primero es colocar una portada básica que lleve todos los datos de la asignación:
- Año académico
- Sección
- Nombre y Apellido del estudiante
- Número de la asignación (#1)
- Fecha de entrega
Ejercicios:
Para cada uno de los siguientes planteamientos, debe representar el segmento AB en el plano, determinar su longitud, calcular y representar su Punto Medio y finalmente determinar la pendiente asociada al segmento.
- A(-7,-4) y B(6,5)
- A(-4,8) y B(5,-2)
- A(-5,3) y B(4,-3)
- A(-6,2) y B(7,6)
- A(-4,4) y B(7,7)
Condiciones de elaboración y entrega de la asignación:
- Debe ser realizada a mano.
- Debe llevar los datos solicitados en la portada
- El plazo máximo de entrega es hasta el 13-14 de abril. (Todo el día).
- Las consultas finalizan el viernes de la semana previa a la entrega de la asignación.
- La asignación debe ser fotografiada y enviada al docente únicamente al correo electrónico.
- Pueden enviar el trabajo como un documento Word o PDF con la portada solicitada y las imágenes adentro.
Enviar al correo electrónico:
ernestovaquero@gmail.com
Dentro de las fuentes de información que hay en Internet, he traído algunas paora que sirvan de apoyo a la lectura de esta publicación.
- Distancia entre dos puntos (longitud del Segmento): Video distancia entre dos puntos
- Punto medio de un segmento: Video Punto Medio
- Pendiente a partir de dos puntos: Video pendiente de un segmento
Esto es todo por el tema de análisis en el plano.
Hasta la próxima entrada, y espero sus consultas.
¡Si todos colaboramos, la tempestad pasará en menos tiempo, y volveremos a la normalidad. Mantengámonos unidos!
M.Sc. Ernesto Vaquero
Matemáticas UEP Kalil Gibrán

















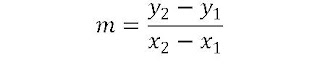


No hay comentarios:
Publicar un comentario